Memoize

As our applications grow and begin to perform more computationally intensive tasks, the need for processing speed increases, and optimization of processes becomes necessary. When we ignore this (optimize our code), we end up with programs that consume a lot of time and use a terrible amount of system resources during execution.

What is Memoization?

Memoization is an optimization technique that speeds up applications by storing the results of function calls (which these functions are called expensive function) and returning cached results when the same request input (which has been executed at least once before).

What is an expensive function?

Make no mistake, we are not spending money here. In the context of computer programs, the two main resources we have are time and memory. Therefore, it is một gọi hàmexpensive to call a function that consumes large amounts of these two resources during execution due to heavy computation (jagged code or complex requests, for example).

For this, memoization uses caching to store the results of function calls, so that they can be quickly and easily accessed later.

A cache is simply a temporary data store that holds data so that it can be served faster for future requests.

Why is memoization necessary?

We have an example as follows:

Imagine you are reading a new novel with an attractively decorated cover at the park. Every time a person passes by, they are attracted by the cover of the book, so they ask the name of the book and its author. The first time the question is asked, you turn the cover page and read the title and the author's name. Now, more and more people keep stopping and asking the same question. You are a very very nice person, so you answer them all

=> You can turn the cover, read the title and author's name for each of them, or you will start memorizing the information and respond to them with your head (instead of turning the cover to read =)) ) Help you save more time? (but still a nice person :v)

This is an example set by the author, suppose there is a guy who reads a book and can't remember the name of the book or the author's name, but actually I'm the same, the book I re-read the most times is Rừng Nauy, remember everything. The character's name but I can't remember the author's name, I say that to prove that the author's example of this article is not very funny.

Notice the similarity? With memoization, when a function is given input, it performs the necessary calculation and caches the result before returning the value. If the same input is received in the future, it will not have to do it over and over again but will simply deliver the result from the cache too.

How does memoization work?

Concepts memoizationin JavaScript are built mainly on two concepts:

• Closures

• Higher Order Functions (returning functions from functions)

• The scope is where a variable or function can be accessed and used/referenced via name directly. And outside that scope, that variable or function will no longer be visible directly.

• Closure is a function or reference (also known as a closure) that comes with the environment it refers to (quite a twist).

As we just said above, scope is the concept that regulates the "visibility" and "lifetime" of a variable. Normally, for example in C, the scope will be block scope, which means that the variables created in the block will only be seen in that block, and when outside of that block, the variables in the block will be released (like in C). are variables created in the stack that will be free when exiting the block), and will no longer be visible.

However, it is sad that our javascript does not have such an easy-to-understand scope, but it is function block. Function blockWhat is this: that is, what you create in a function will be available in that function. Since javascript is also block syntax, it can be a bit confusing, we will use this easy to understand example:

function scope() {
  if (true) {
    var test = 1;
  }
  alert(test); #=> 1
}
scope();

Talking about this, you will definitely think about what happens when we have nested functions. Let's try:

function outer() {
  var outer_var = 2;
  function inner() {
    alert(outer_var);
  }
  inner();
}
outer(); #=> 2

From the above example we can easily see that variables inner functioncan be accessed outer function. From this example we can see that inner functionwe can inherit the variable of outer function, or in other words, i nner functioncontains (contain) scopeof outer function.

A closure is an expression (typically a function) that can have free variables together with an environment that binds those variables (that "closes" the expression).

Maybe some of you will wonder, environmentwhat is here? To visualize it in an easy-to-understand way, environmenthere in most cases is the outer function that we just tried in the scope example above. A nice feature of closures is that the closure will keep references to variables that are inside it, or called within it. What does this lead to? Perhaps you will think of a very special case when you want the context of a function to be retained after that function has been executed. Let's start with an example:

function outside(x) {
  function inside(y) {
    return x + y;
  }
  return inside;
}
fn_inside = outside(3); 
result = fn_inside(5); // #=> 8

result1 = outside(3)(5); // #=> 8

Did you notice anything special above? The special thing is in the function fn_inside: the function fn_insideis created by the return result of the function outside()with parameter 3, and you can see that the function fn_insidestill keeps a reference to parameter 3 even after the function outside()has been executed. You will probably see a contradiction with the theory of function scope we talked about above, when everything created in a js function can only be seen and used within it, and will be released or not visible when outside that function. In fact, there is no contradiction at all, because of the so-called closure of js. To be more specific: fn_insidewhen created, a closure is also created, in that closure, the value 3 is passed in, and the closure fn_insidewill retain that value 3 for as long as possible. even though outside()the function has finished executing.

=> This is the key issue for us to learn more about in the next section.

The above paragraph is copied from the article Closure and scope in javascript

Case Study: Fibonacci number sequence

What is the Fibonacci sequence?

• is a sequence of numbers starting from 0 or 1, and the following numbers are the sum of the two numbers before it.

• For example:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
// hoặc
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

The classic problemn is: write a function to find the third number of a series of numbers.

And first we immediately think of a recursive function:

function fibonacci(n) {
    if (n <= 1) {
        return 1
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Concise and very precise! But, there's a problem. Note that in continuously reducing the size of the problem (the value of n) until the final case is reached, a lot of work will be done and it will take time to arrive at the final result, because there is a repeated calculation of certain values ​​in the series. Looking at the diagram below, when we try to calculate fibonacci(5), we continuously look for Fibonacci numbers at indices 0, 1, 2 and 3 on different branches. This is called redundant computation and is exactly what that memoizationeliminates.

Now we will refactor the code with memoization:

function fibonacci(n,memo) {
    memo = memo || {}
    if (memo[n]) {
        return memo[n]
    }
    if (n <= 1) {
        return 1
    }
    return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
}

In the code above, we adapt the function to accept an optional parameter called memo. We use the object memoas a cache to store the Fibonacci numbers with their corresponding indices as keys, so that we can retrieve them whenever they are required in subsequent calculations.

memo = memo || {}

Here, we check whether memoit is passed in or not. If it is, we will initialize it for use, but if not, we will set it to an empty object.

if (memo[n]) {
      return memo[n]
}

Next, we check to see if there is a cached value for the current key n? and returns its value if available. As in the previous solution, we specify the end case when nless than or equal to 1.

Finally, we recursively call the function with the nsmaller value, while passing the cached values ​​( memo) into each function, to be used during the calculation. This ensures that once the value has been previously calculated and cached, we do not perform such a calculation a second time. We are simply retrieving the value from the cache. Note that the final result must be added to the cache before returning it.

It seems okay, let's try to calculate the results and check the performance?

Performance testing with JSPerf

Read How does jsPerf work? To understand more about jsperf, ops/sec is the number of calculations performed in 1 second.

Here we perform performance testing with calculationsfibo(20)

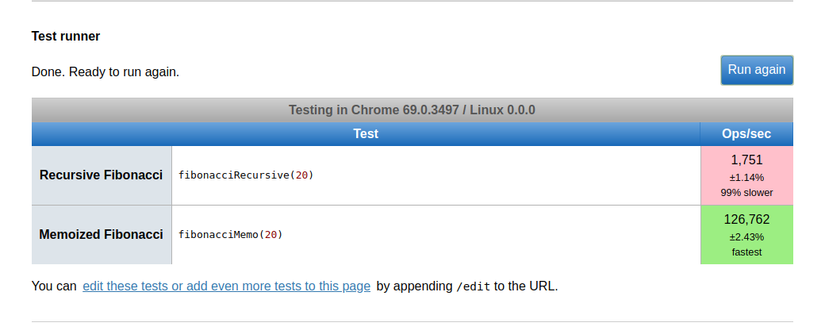
We can see it is very impressive, when pure recursive code only operates at a speed of 1,751 ops/sec, 99% slower than using memoization with 126,762 ops/sec.

So to achieve such impressive results. We have to add cache memoto each function, modify them a bit to achieve the desired result? Not really, we will use the feature returning functions from functionsmentioned above to memoize any function we want.

A Functional Approach

In the code below, we create a higher order function called memoizer. With this function, we will be able to easily apply memoization to any other function:

function memoizer(fun) {
    let cache = {}
    return function (n) {
        if (cache[n] != undefined ) {
          return cache[n]
        } else {
          let result = fun(n)
          cache[n] = result
          return result
        }
    }
}

Above, we just need to create a new function called that memoizeraccepts the function funas parameter. In the function, we create a cache object cacheto store the result of function execution, for future reuse.

From the function memoizer, we return a new function that can access the cache regardless of where it is executed, due to the closure principle discussed above. And similar to the previous example, we calculate and cache the results cachebefore returning the results.

Testing memorizer function

We compare the results memoizerwith the above cases, we have:

And our processing memoizerspeed is ~42 million ops/sec, approximately 100% faster than other methods. (okay)

It's very possible that the author's computer is faulty, my computer gave results of up to 303 million ops/sec, below are the test results on my computer (however, the ratio between the processing methods is still approximately the same. Stop)

When should I use memorizer?

Here are three situations in which this memoizationwould be beneficial:

• As for function calls expensive function, i.e. functions that perform heavy calculations.

• For functions with a limited and highly recurring input range, such that cached values ​​not only stay put but also do not change at all.

• For recursive functions with recurring input values.

• For pure functions, that is, functions that return the same output every time they are called with a particular input.

The library uses memoization

• Lodash Memoize
• Memoizer
• Fast Memoize
• Moses
• Reselect for Redux